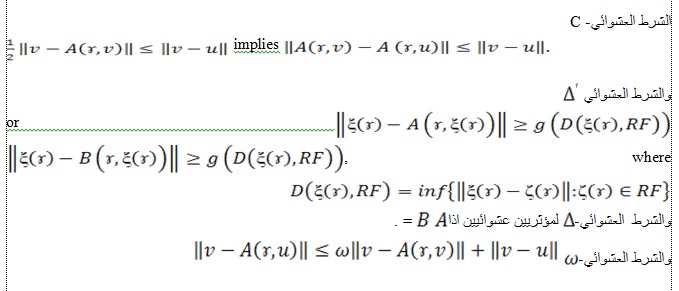قسم الرياضيات يناقش رسالة اطروحة دكتوراه تبحث في مبرهنات تقارب النقطة الصامدة العشوائية

ناقش قسم الرياضيات في كلية التربية للعلوم الصرفة (ابن الهيثم) اطروحة الدكتوراه الموسومة (مبرهنات تقارب النقطة الصامدة العشوائية مع تطبيقاتها ) للطالب ( صباح حسن مالح ) التي انجزها تحت اشراف التدريسية في القسم ( أ.م.د. سلوى سلمان عبد ) ونوقشت من قبل لجنة المناقشة التي تألف من الاعضاء المدرجة اسمائهم فيما يأتي :

• أ.د. سميرة  ناجي كاظم                  ( رئيسا )

• أ.م.د. عماد عباس كوفي                 ( عضوا )

• أ.م.د. يوسف يعكوب يوسف           ( عضوا )

• أ.م.د. معن عبد الكاظم رشيد       ( عضوا )

• أ.م.د. نيران صباح جاسم                ( عضوا )

• أ.م.د. سلوى سلمان عبد               ( عضوا ومشرفا )

تهدف هذه الاطروحة إلى دراسة التقارب (القوي / الضعيف) لبعض انماط العمليات التكرارالعشوائي المعرفة لانماط مختلفة من المؤثرات العشوائية غيرالتوسعية. المؤثرات التي سيتم تبنيها هنا هي غيرتوسعيية وشبه غير التوسعية  وشبه غيرالتوسعية الرتيبة وبعض التعميمات الأخرى للمؤثرات العشوائية غيرالتوسعية ،مثل

حيث A , B  مؤثريين عشوائيين في فضاء بناخ القابل للفصل .في اي فضاء اختياري بناخ القابل للفصل ، نقوم أنشاء مخططات تكرارية عشوائية مختلفة للمؤثرات المذكورة أعلاه مثل : تكرار العشوائي فيبوناشي -مان (  لخطوة واحدة وخطوتين) والتكرار العشوائي ( خطوتين أنوبام شارما ومحمد إمداد (RABI), ، خطوتين مع تطبيق التراجع أنوبام شارما ومحمد إمداد (RPI)، وثلاث خطوات أنوبام شارما ومحمد إمداد (RNSI), وخطوتين كراول(RSI)  )

خلال هذاالعمل ، تتم دراسة تقارب هذه المخططات التكرارية الى النقاط الصامدة العشوائية والنقاط الصامدةالعشوائية المشتركة والتي تتطلب امرين وهما إثبات بعض مبادئ شبه الإنغلاق للمؤثرات قيدالمناقشة وتقديم العديدمن المفاهيم المتراجحات والعلاقات في حالةالمؤثرات العشوائية.تجدرالإشارةهنا إلى أنه يتم أيضًا عرض النتائج المتعلقة باستقرارإجراء تكرارالنقطة العشوائية المرتبطة بالمؤثرات المذكورة اعلاه. أخيرًا ، تتضمن الأطروحة إثبات وجود وتفرد الحل لمعادلة  تكامل عشوائية.

---

Approximating Random Fixed Point Theorems with Applications

By Sabah .H.Malih

Supervised by Asst.prof.Dr.Salwa.S.Abid

Abstract

Random nonlinear analysis is an important mathematical discipline which is mainly concerned with the study of random nonlinear operators and their properties and is much needed for the study of various classes of random equations.This thesis aims to study the convergence (strong/ weak) of some types of random iteration processes under various random nonexpansive operators. The operators that will be adopted here are nonexpansive, asymptotically nonexpansive, monotone asymptotically nonexpansive and some other generalizations of random nonexpansive operators such as,

Random C-condition: implies

Random -condition:or wher

Random -condition: if one operator =    

Random-where are random operators on a separable Banach space .In the arbitrary separable Banach space, we construct different random iterative schemes for the above operators which are random Fibonacci–Mann (one-step and two-step) scheme, random two-step Anupam Sharma and Mohammad Imdad (RABI) scheme  two operator, random two-step with retraction mapping Anupam Sharma and Mohammad (RPI) scheme, random three step Anupam Sharma and Mohammad (RNSI) scheme and random two step Agarwal (RSI) scheme.  Throughout this work, the convergence of these iterative schemes to random fixed points and common random fixed points is studied which requires two things which are proving some principles of semi-closedness for the operators under discussion and presenting many concepts, inequalities and relations in the setting of random operators.It is worth mentioning here, the results concerning the stability of random fixed point iteration procedures associated above operators are also presented. Finally, the thesis includes proving the existence and uniqueness of the solution to a random integral equation